Bose-Einstein-Kondensate aus Photonen: Statistische Physik
Was ist ein Bose-Einstein-Kondensat?
Wir haben die Teilenzahlstatistik des im Farbstoff-Mikroresonatorsystem erzeugten Photonenkondensats bestimmt. Für kleine Photonenzahlen werden dabei für den kondensierten Zustand ungewöhnlich hohe Werte der normierten Intensitätskorrelation von bis zu g(2)(0) =1,7 beobachtet, was sich erheblich von dem bei üblichen Bose-Einstein-Kondensaten oder auch bei Lasern beobachteten Wert g(2)(0)=1 unterscheidet. Grund für diese erhöhten Schwankungen der Teilchenzahl ist, dass das Photonenkondensat effektiv Teilchen mit den photo-anregbaren Farbstoffmolekülen austauschen kann, was gut im Bild des großkanonischen Ensembles beschrieben werden kann. Die Messungen liefern direkte Beweise für ein großes kanonisches Bose-Einstein-Kondensat. Für hohe Kondensat-Teilchenzahlen, oder auch für kleine Molekülzahlen, wird wieder der übliche Wert g(2)(0)=1 beobachtet, was dann einem kanonischen Ensemble entspricht.
In anderen Arbeiten haben wir die Wärmekapazität von kondensiertem Licht bestimmt. In diesem Zusammenhang untersuchen wir Effekte der statistischen Mechanik von Quantengasen.
J. Klaers, J. Schmitt, F. Vewinger, and M. Weitz, Phys. Unserer Zeit 42, 58 (2011)
J. Klaers and M. Weitz, in Novel Superfluids, Vol. 1, K. H. Bennemann and J. B. Ketterson (Eds.) (Oxford University Press, Oxford, 2013), arXiv: 1210.7707
E. Busley, L. Espert Miranda, M. Weitz, and J. Schmitt, Phys. in unserer Zeit 53, 166 (2022)

Nahaufnahme des Resonatoraufbaus. Ein Tropfen Farbstofflösung befindet sich zwischen den beiden hochreflektierenden Spiegeln, hier sichtbar durch die helle gelb-rote Fluoreszenz in der Mitte. Durch die Prismen auf der Spiegelrückseite wird das Pumplicht in den Resonator geführt.
Photonen in Box-Potentialen
In diesem Projekt untersuchen wir die statistische Physik von Photonenkondensaten in Kastenpotentialen. In einem Kasten kann der Grundzustand makroskopisch besetzt sein, ohne dass ein Phasenübergang stattfindet, d. h. es gibt keine Diskontinuität in einer thermodynamischen Größe wie der spezifischen Wärme. Da das System homogen ist, kann man mechanische Eigenschaften wie die Kompressibilität extrahieren.

Künstlerische Darstellung von Photonen in einer Schachtel
Fluktuierendes Photonengas
Die Fluktuations-Dissipations-Relation ist ein Eckpfeiler der statistischen Physik, der die Fluktuationseigenschaften mit Gleichgewichtseigenschaften wie der Kompressibilität in Beziehung setzt.

Das Photonengas im Mikroresonator weist ungewöhnliche Fluktuationseigenschaften auf, die sich in der "körnigen Struktur" des Gases zeigen. Bei großen Reservoirs werden die Fluktuationen stärker als üblich, und die Fluktuationen können so groß wie die durchschnittliche Photonenzahl werden.
Photonengase in einer Dimension
Bei der Betrachtung von Quantengasen unterscheiden sich eine und zwei Dimensionen deutlich. In zwei Dimensionen erwartet man einen echten Phasenübergang für ein harmonisch eingefangenes Gas, während in einer Dimension ein Einfangpotenzial erforderlich ist, das stärker als linear ist. In diesem Projekt untersuchen wir den Übergang von 1D zu 2D, indem wir Mikrostrukturen auf Polymerbasis auf einem der Spiegel verwenden, um das Photonengas einzufangen.
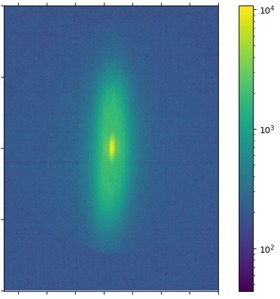
Emission aus einem mikrostrukturierten Potential, die vertikale Achse entspricht etwa 100 µm.
Key publications:
J. Klaers, J. Schmitt, F. Vewinger, and M. Weitz, Nature 468, 545 (2010).
J. Schmitt, T. Damm, D. Dung, F. Vewinger, J. Klaers, and M. Weitz, Phys. Rev. Lett. 112, 030401 (2014)
E. Busley, L. Espert Miranda, A. Redmann, C. Kurtscheid, K. Karkihalli Umesh, F. Vewinger, M. Weitz, J. Schmitt, Science 375, 6587 (2022)
F. Emre Öztürk, T. Lappe, G. Hellmann, J. Schmitt, J. Klaers, F. Vewinger, J. Kroha, M. Weitz, Science 372, 6537 (2021)
